1. 공개 키 알고리즘
대칭 키 알고리즘의 문제점
- 키 분배가 어려움
- 소통하는 사람마다 대칭키가 달라서 많은 키가 생성됨 ( Key 갯수 : (n*(n-1)) / 2 )
공개 키 알고리즘 : 메시지를 공캐키&비밀키 쌍을 사용하여 암&복호화 한다.
- 공개키로는 개인키로 암호화된 메시지를 복호화 할 수 있다.
- 유사하게 개인키도 공개키로 암호화 된 메시지를 복호화 할 수 있다.
공개 키 암호화
- 1970년도에 제안된 알고리즘으로 개인키로 공개키를 유추하기 어렵고 chosen-plaintext 공격에 강하다
- RSA에서 가장 흔히 사용되는 공개 키 알고리즘
- 일반적으로 대칭키 알고리즘보다 훨씬 느리다 ( 메시지 자체를 암호화는 데 주로 사용되지 않음 )
공개 키 암호화 응용 프로그램
[1] 암호화 & 암호 해독
- 발신인이 수신인의 공용 키로 메시지를 암호화한다.
- 수신자는 개인키로 암호문을 해독함
[2] 디지털 서명
- 발신인이 개인키로 메시지에 서명을 함
- 수신자는 발신인의 공용 키로 메시지 서명을 확인함
[3] 키 분배
- 송신자가 세션 키를 생성하고, 수신자의 공용 키로 세션 키를 암호화하여 수신자에게 전송함
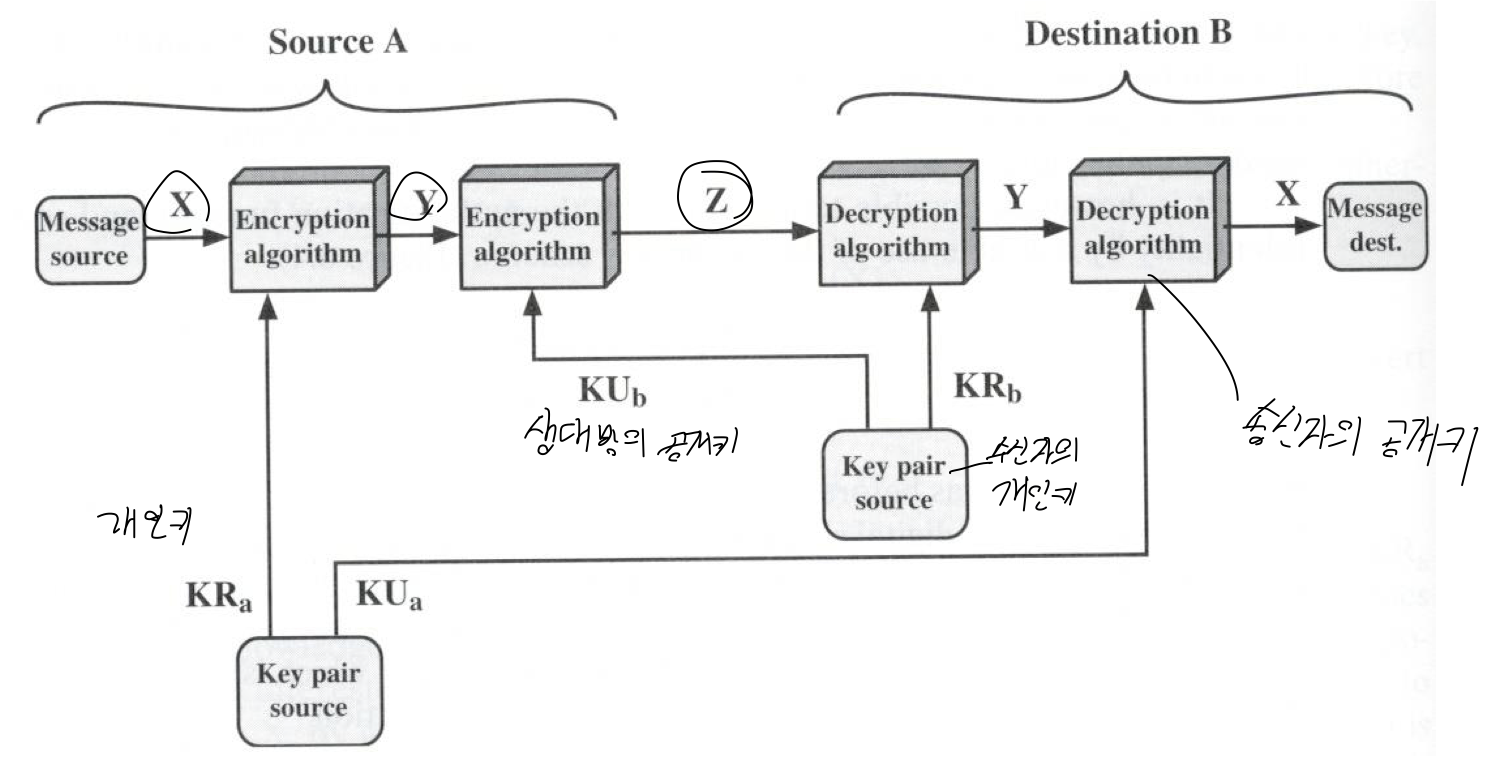
[4] 대칭 키 & 공개 키 접근 방식의 하이브리드 형식
- 공개 키 암호 시스템을 사용하여 세션키를 만들고 이를 peers들 사이에 배포함
- 세션키를 통해서 메시지를 암호/복호화 한다.
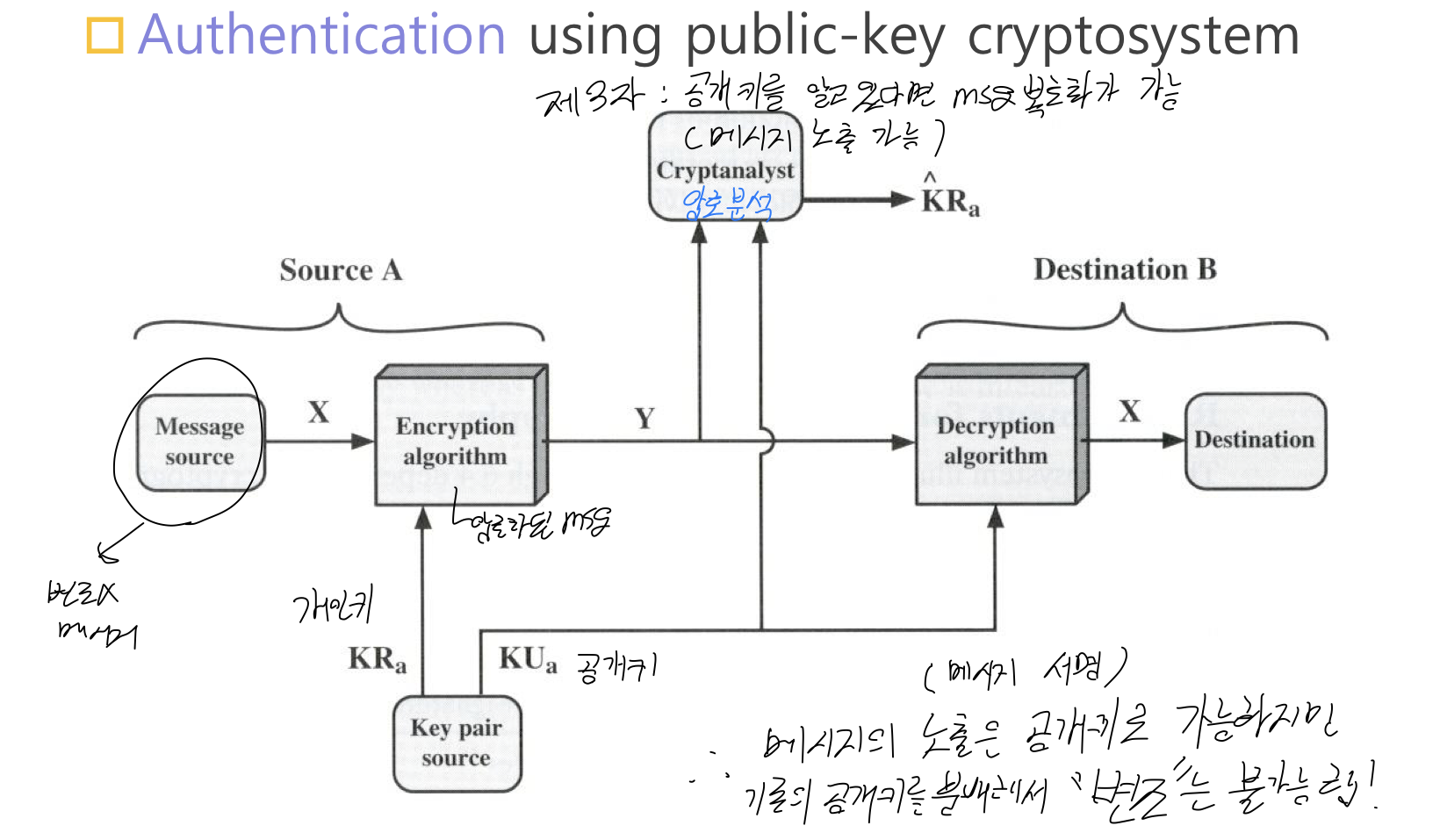
=> 3자가 서로 간의 공캐키를 알고 있다면 전송 중간에 가로채서 Msg를 복호화 하는 것이 가능 ( 메시지 내용 노출 가능 )
=> 하지만 개인키로 암호화 되어 있기 때문에 개인키를 알지 못하면 암호화해서 전송할 수 없음 ( 변조 불가능 )
공개 키 암호화의 요구사항
- 적절한 시간 내에 키 생성이 완료되어야 함
- 송신자가 메시지를 암호화 하고 전송하는데 용이해야 함
- 수신자가 암호화 된 메시지를 복호화 하는데 용이해야 함
- 어택커가 알려진 공개 키를 통해서 개인 키를 알아내는 것은 계산상 불가능 해야 한다.
- 어택커가 공개 키를 통해 메시지를 복호화하는 것이 계산상 불가능 해야 한다.
RSA ( Rivest, Shamir, and Adleman )
인수분해를 기반으로 만들어진 공개 키 암호화 기법
- 엄청나게 큰 수의 인수분해 하는데 비용이 많이 드는 것을 이용한 기법
- 계산 복잡성은 지수화에서 비롯된다.
- 가장 큰 수의 소수 p, q를 사용한다 ( N = p*q , Z=(p-1)(q-1) )
- n보다 작은 e와 z를 선택한다. 각 값은 서로소여야 한다.
- ed ≡ 1 (mod z) 인 d를 찾는다.
- 이렇게 되면 공개 키는 ( n,e ) , 비밀 키는 ( n,d )
| RSA - 공개 키 ( n , e ) - 비밀 키 ( n , d ) |
|
| 원문 M 을 암호화 | C = M^e (mod n) |
| 암호문 C를 복호화 | M = C^d (mod n) |

Hybrid
공개 키는 통신 효율성 측면에서는 좋지만 속도가 느리다
대칭 키는 빠르지만, 많은 키가 필요하고 세션 키를 공유하기 어렵다
하이브리드는, 대칭 세션 키는 송신자에 의해 생성되고, 수신자의 공개 키로 암호화 되어 수신자에게 전송된다. 그 후 세션 키와 추가 통신이 이루어짐
공개 키 분배
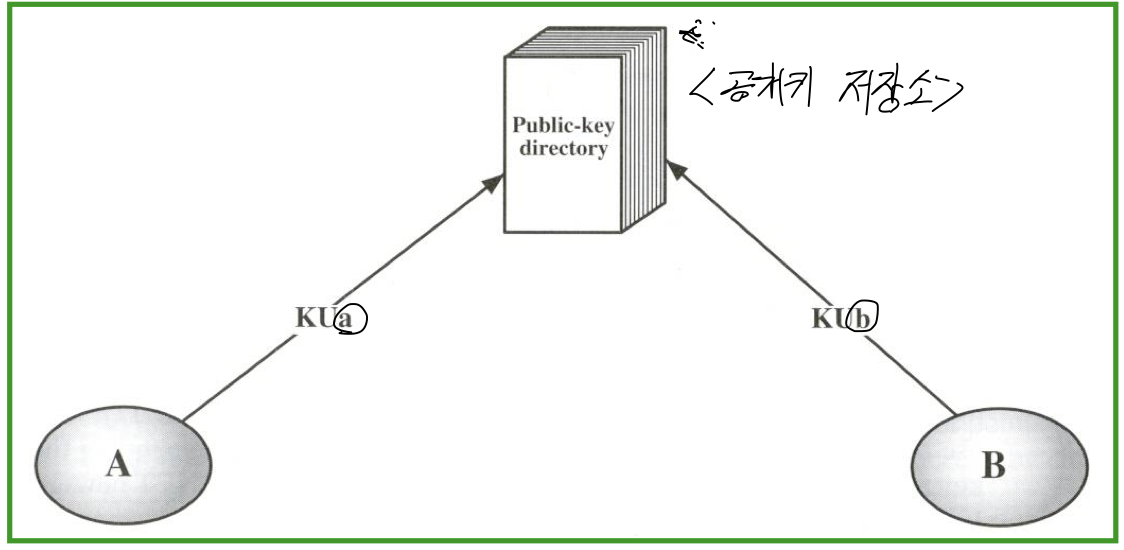
[1] 공개 키 디렉토리 ( public-key directory ) 를 이용하는 방법
- 공개 키 디렉토리에서 ( ID , KUID ) 쌍을 유지하고 관리함
- 각 구성원이 공용 키를 생성하고 공용 디렉토리에 등록함
- 각 구성원이 다른 사람의 공개 키를 얻기 위해 저장소에 엑세스 함
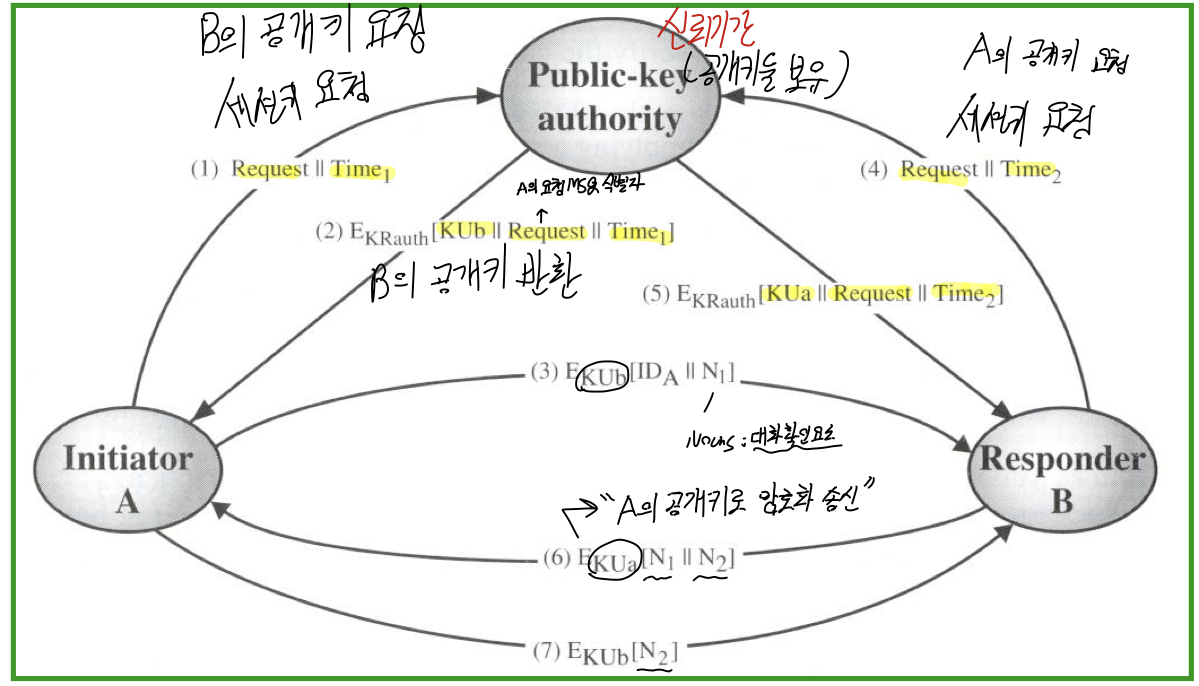
[2] 공개 키 신뢰기관 ( public key authority )
- 공개 키 디렉토리에서 공개 키의 보안&배포를 관리한다.
- 각 peer는 공개 키 기관의 공개 키를 알고 있다.
[3] 공개 키 인증서
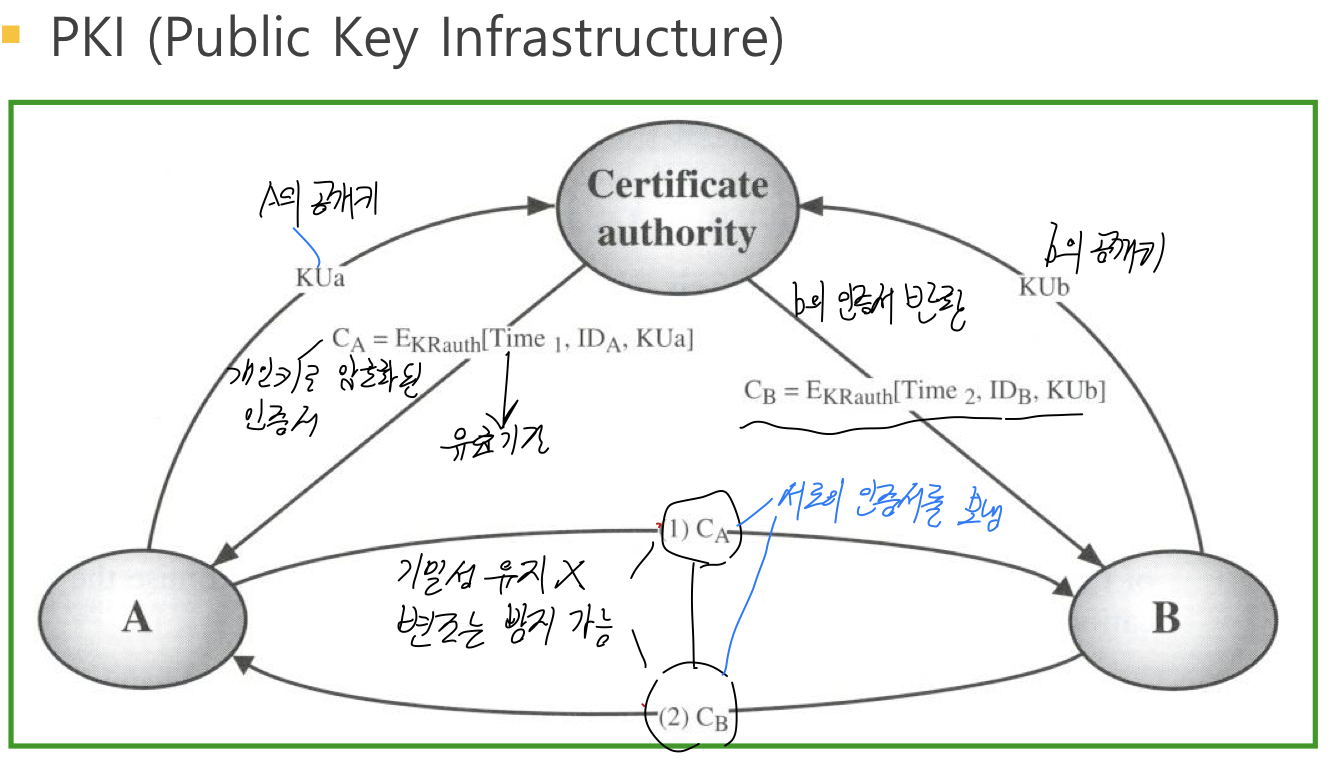
Diffie-Hellman Key Distribution
- 이산 로그의 계산이 어려운 것을 이용한 알고리즘
- q : 큰 수의 prime number
- a : a < q and q의 primitive root ( 원시근 )


Diffie-Hellman 공개 키 알고리즘은 세션 키 교환으로 제한된다.

그밖의 공개 키 암호화
DSS ( digital signature standard )
- 디지털 서명 기술로 SHA-1 해쉬 알고리즘을 사용함
ECC ( Elliptic curve cryptography )
- 타원 곡선 함수를 이용한 알고리즘
2. Authentication [ 인증 ]
메시지의 송 수신자와 변조의 여부를 확인하는 검증 과정
요구 사항
- 메시지는 명백한 출처가 있는지 또는 신뢰하는 peer에게 왔는지
- 내용이 변경되지 않았음을 보장할 수 있는지
- 때때로 , 특정 시간과 순서에 따라 보내진 것을 보장할 수 있는지
인증 방법
- 일반 암호화를 이용한 메시지 인증 : 발신자와 수신자만 키를 공유해야 한다.
- 메시지 암호화 없는 메시지 인증 : 인증 태그가 생성되어 각 메시지에 추가된다.
- 메시지 인증 코드 (MAC) : 메시지와 키의 함수로 MAC 계산을 이용한다 : MAC = F(K,M)
MAC을 사용한 메시지 인증
: 메시지가 노출되어도 상관 없고 , 변조의 유무만 체크 할 겨우 사용된다.
Messsage Authentication
 |
 |
| MAC을 사용한 Message 인증 - 메시지 노출 체크 X - 메시지 변조 유무 체크 가능 |
hashed MAC을 사용한 Message 인증 - |
 |
 |
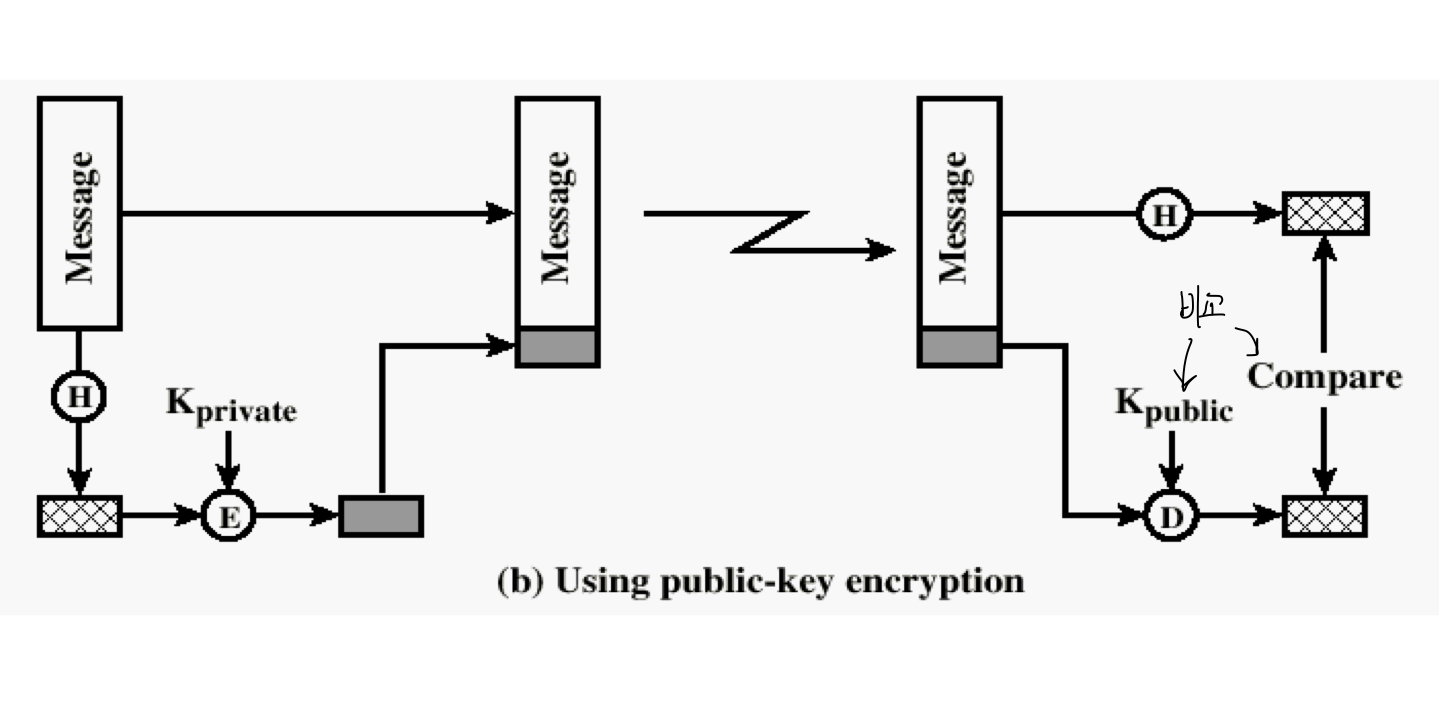
| MAC을 사용한 Message 인증 - 공개 키를 사용한 암호화 |
Hashed MAC과 secret value를 사용한 Message 인증 -hash 전에 시크릿 값이 추가되고, 전송 전에 제거된다 |
HASH 함수
지문을 생성하는 것
"H"ash의 속성
- H는 데이터 블록의 어떤 크기든 적용될 수 있어야 한다.
- H는 고정된 길이의 출력을 제공해야 한다.
- H(x)는 주어진 x에 대해서 계산하기 쉬워야 한다.
- 같은 해쉬 y가 나오는 x를 찾는 것이 어려워야 한다.
HMAC : SHA-1과 같은 암호화 해시 코드에서 생성된 hashed MAC의 시크릿 값
동기
- DES, AES 등 암호화 알고리즘 보다 빠른 암호화 해시함수를 실행함
- 암호화 해시함수 라이브러리 코드가 범용적으로 사용 가능
반응형
'Lab & Research > Information Security' 카테고리의 다른 글
| 이메일 보안 ( PGP , S/MIME ) (0) | 2022.05.09 |
|---|---|
| 메시지 인증 & Kerberos & PKI (0) | 2022.04.16 |
| 네트워크 접근 제어 & 클라우드 보안 (0) | 2022.04.15 |
| Web : SSL&SSH&SET (0) | 2022.04.13 |
| 대칭 암호화 & 메세지 기밀성 (0) | 2022.03.17 |



