1. Linear Regression
예측 값을 직선으로 표현하는 모델


예측값 = 편향 + { 계수 * 입력값 }
회귀 직선으로 나타낼 경우, x값의 증감에 따라 예측 값이 증가하는 정도를 알 수 있어서, 해석하기에 용이함
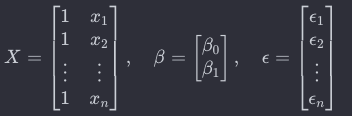
선형 회귀의 평가
실제 값과 예측 값의 차이가 작은 직선이 데이터를 더 잘 표현한다고 할 수 있다.
1. 평균제곱오차-MSE ( Mean Squared Error )
- 실제값과 예측값의 차이를 제곱한 후 평균화함
- 예측값과 실제값 차이의 면적의 평균과 같음
- 특이값이 많이 존재할 수록 수치가 많이 늘어난다.
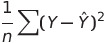
2. 평균절대오차
- MAE는 예측값과 실제값 간의 절대적인 차이를 나타냄
- 각 데이터 포인트에서 예측값과 실제값의 차이를 모두 더하고, 그 값을 전체 데이터 포인트 수로 나누어 구함.
- MAE는 이상치에 민감하지 않은 특징이 있습니다. 즉, 이상치가 모델의 성능에 큰 영향을 미치지 않음
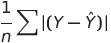
두 지표 모두 모델의 예측 성능을 측정하는 데 사용되지만, 선택은 주로 문제의 특성과 모델의 목적에 따라 달라집니다.
MAE는 이상치에 덜 민감하고 직관적이지만, MSE는 큰 오차에 대해 더 큰 페널티를 부여하므로 모델이 미세한 차이에 민감한 경우 사용될 수 있습니다. MSE는 회귀에서 손실 함수로서 자주 사용하고, 회귀 지표로 MAE를 주로 사용한다.
2. Multivariate Regression
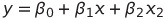
다변량 회귀 : 2개 이상의 변수를 통해서 만들어지는 회귀식을 말함.
( 변수가 여러개인 경우 행렬로 표현함 )
| 선형 회귀 | pred = β0 + β1 * x |
| 다변량 회귀 | pred = β0 + ( β1 * x ) + ( β2 * y ) |
변수가 3개인 경우 : pred = β0 + ( β1 * x1 ) + ( β2 * x2 ) + ( β3 * x3 )
==> y = βX + ϵ 로 나타낼 수 있다.
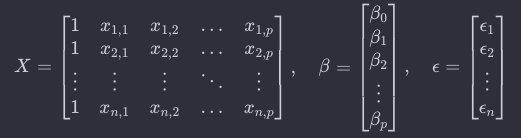
X는 데이터의 특징(독립변수)을 담은 행렬이며, 각 행은 데이터 포인트를 나타내고 각 열은 특징을 나타냅니다.
행렬에서 첫 번째 열은 항상 1로 채워지는데, 이는 절편( β )을 나타냅니다.
변수의 절편에 따라서 어떤 변수가 예측에 더 중요한 영향을 끼치는지에 대해서 알 수 있다.
3. Polynomial Regression

다항식 회귀 : 예측하는 값이 선형이 아닌, 비선형일 경우에 사용함
X의 몇 제곱이냐에 따라서 비선형성을 늘릴 수 있음

회귀 계수를 계산 방법론
1. 통계적 방법
최소 제곱 법 : y = βX
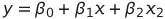
최소제곱법으로 구한 β Equation :
2. ML적 방법
- 여러 값을 넣어 본 뒤, Loss(MSE)가 제일 작은 β 를 찾는다.
- 효율적으로 여러 값을 넣어 β 를 찾는 것을 최적화 알고리즘이라 한다.
2-1 ) Bisection Metod 방법
- 임의의 x 두 값을 설정
- 두 값의 y 값을 비교하고 y값이 큰 점을 두 점의 가운데 점으로 바꾼다
- 임의의 두 값의 차이가 작아질 때 까지 1~2를 반복한다.
2-2) Gradient Descent
- 함수의 기울기를 구하고 경사의 절대값이 낮은 쪽으로 게속 이동시켜 극 값에 이를 때까지 반복시키는 것

- 임의의 값 하나를 설정한다.
- 임의의 값의 기울기를 계산한다
- 기울기와 Learning Rate를 곱한 값을 임의의 값에서 뺀다.
- 기울기가 0에 가까워질 때 까지 1~3을 반복한다.
4. Code
4-1 Linear Regression
np.random.seed(2023)
x = np.array([1,2,3,4])
y = np.array([2,1,4,3])
# 사이킷런에서 학습 데이터는 (n,c) 형태로 되어야 함
# - n: 데이터의 갯수
# - c: feature의 갯수
data = x.reshape(-1,1) # (4,1) ==> (4,1)
from sklearn.linear_model imports LinearRegression
model = LinearRegression()
model.fit(X=data, y=y)
model.intercept_ # 편향 확인
model.conf_ # 회귀 계수 확인
pred = model.predict(data) # 학습된 모델 예측
4-2 Multivariate Regression
bias = 1
beta = np.array([2,4,3,5]).reshape(4, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 4)
y = bias + X.dot(beta)
y_with_noise = y + noise
model = LinearRegression()
model.fit(X, y_with_noise)
4-3 Polynomial Regression
bias = 1
beta = np.array([2,3]).reshape(2, 1)
noise = np.random.randn(100, 1)
X = np.random.randn(100, 1)
X_poly = np.hstack([X, X*2])
y = bias + X_poly_dot(beta)
y_with_noise = y + noise
model = LinearRegression()
model.fit(X_poly, y_with_noise)
5. Regularization
- 과적합 문제를 해결하자
- 불필요한 β에 대한 학습을 방지

선형 회귀의 목표
- 실제 값을 잘 예측 { Loss를 최소화 시키는 것 ) ==> ( argmin(y-βX)^2 }
- 이 때, 과적합을 방지하기 위해 불필요한 beta는 학습하지 않도록 해야 함
선형 회귀의 정규화
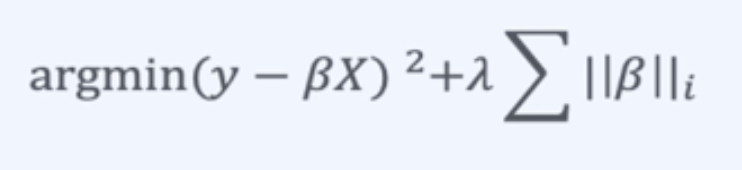
||β||_i : 계수들의 norm을 의미함
L1 Norm : 벡터의 각 성분을 절대값 취한 뒤 전부 더한 값
- L1 Norm을 이용한 정규화의 종류로는 LASSO가 있음
- 필요 없는 β를 0으로 만듬


L2 Norm : 벡터의 각 성분을 제곱 한 뒤 모두 더한 값의 제곱근
- L2 Norm을 이용한 정규화의 종류로는 Ridge가 있음
- 필요 없는 β를 아주 작은 값으로 만듬
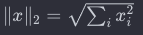

L1 Norm과 L2 Norm은 벡터의 크기를 측정하는 방법 중 두 가지 주요한 방법
L1 Norm (맨해튼 Norm 또는 Taxicab Norm) 은 벡터의 각 성분의 절대값을 더함
장점:
- 희소성(Sparsity): L1 Norm은 일부 성분을 0으로 만들어 희소한 모델을 유도할 수 있습니다. 이는 feature selection에 유용할 수 있습니다.
- 로버스트성(Robustness): L1 Norm은 이상치(outliers)에 상대적으로 덜 민감하다는 특성이 있습니다.
단점:
- 비유연성: L1 Norm은 미분이 불가능한 점이 존재하므로 최적화 알고리즘이 복잡해질 수 있습니다.
L2 Norm (유클리드 Norm) L2 Norm은 벡터의 각 성분을 제곱하고 더한 후 제곱근을 취한 값
장점:
- 미분 가능성: L2 Norm은 어떤 점에서든 미분 가능하므로 최적화에 용이합니다.
- 유연성: L2 Norm은 각각의 성분에 대해 연속적인 가중치를 부여하므로, 각 특성이 모델에 미치는 영향을 고르게 측정할 수 있습니다.
단점:
- 비희소성(Sparsity): L2 Norm은 희소한 모델을 생성하지 않습니다. 대부분의 가중치는 0이 아니게 됩니다.
- 이상치에 민감: L2 Norm은 이상치에 민감할 수 있습니다.
특화된 사용 사례
- L1 Norm: Feature selection이 중요한 경우. 모델이 특정 특성에 강하게 의존할 때.
- L2 Norm: Ridge Regression과 같이 가중치를 규제할 때. 데이터가 작은 이상치를 포함하고 있을 때.
일반적으로는 L2 Norm이 더 많이 사용되지만, 상황에 따라 L1 Norm이나 두 Norm을 혼합하여 사용하는 Elastic Net과 같은 방법도 있습니다.
'Lab & Research > Artificial intelligence' 카테고리의 다른 글
| 머신러닝 알고리즘 - Naive Bayes (1) | 2023.12.29 |
|---|---|
| 머신러닝 알고리즘 - Logistic Regression (0) | 2023.12.18 |
| Genetic Alogorithm 의 주요 이슈 (0) | 2023.06.19 |
| Genetic Alogorithm 기초 (0) | 2023.05.21 |
| 진화 연산 개념 (0) | 2023.04.25 |



