1. Encoding
인코딩은 실제 해결해야할 문제를 어떤식으로 chromosome하게 나타내는지에 대해서 다룹니다.
즉, GA에서 사용할 각 solution으로 어떻게 변환하여 나타낼지에 대한 문제로, 다양한 이슈들을 겪습니다.
※ 표현 체계에 대한 문제
– Binary vs k-ary
Binary encoding은 각 gene이 0 또는 1의 값을 가지는 것을 의미하며, 다양한 문제에 유용하게 사용됩니다. 하지만 해결해야 할 문제에 따라서는 k-ary encoding(각 gene이 k 개의 값을 가지는 것)도 적용할 수 있습니다. 예를 들어, 문제에 따라 3 개 이상의 선택지가 필요한 경우 k-ary encoding을 사용할 수 있습니다.

먼저, decimal notation(10진법)으로 인코딩된 gene을 binary encoding(2진법)으로 변환하면 각 gene은 4개의 binary gene으로 표시됩니다.
이러한 변환 작업은 crossover에게 여러 cut points를 제공하여 다양한 후손(generated offspring)을 생성할 수 있도록 해줍니다. 이는 선택 가능한 candidates(후보군)의 개수가 증가하여 offspring 때문에 다양성이 증가하게 됩니다. binary encoding과 k-ary encoding 간에 논쟁이 있을 수 있지만, 이는 mutation operator를 사용하여 유사한 효과를 달성할 수 있기 때문에 의미가 없습니다.
즉, mutation을 통해 chromosome의 다양성을 확보하여 다양한 후손을 생성할 수 있습니다.
(+ Gray Encoding은 인접한 숫자간의 비트가 1씩 차이 나기 때문에 유사도를 인코딩을 통해서 적절하게 나타낼 수 있음 )
– Discrete-valued vs Real-valued
Discrete-valued encoding은 각 gene이 정수나 심볼 등의 이산적인 값으로 인코딩되는 것을 의미합니다. Real-valued encoding은 각 gene이 연속적인 값을 가지며, 가능한 모든 숫자를 포함하는 것을 의미합니다. 이산적인 문제는 Discrete-valued encoding을 사용하며, 연속적인 값을 가지는 문제는 Real-valued encoding을 사용할 수 있습니다. ( 일반적으로 Real-valued 사용 )
– Variable vs invariable
Variable encoding은 서로 다른 길이의 chromosome을 가지는 경우입니다. 각 chromosome이 서로 다른 수의 genes를 가질 수 있습니다. Invariable encoding은 모든 chromosome이 같은 수의 genes를 가지는 경우입니다.
– Locus-based vs order-based
Locus-based vs order-based: Locus-based encoding에서는 각 gene이 일반적인 배열과 같이 특정 위치에 존재하며 해당 위치와 매핑된 값으로 인코딩됩니다. Order-based encoding에서는 각 gene 위치와 값이 서로 다른 면에서 표현되며 이 값은 순서에 따라 인코딩됩니다.
> in Locus, #genotype : #phenotype = 1 : N
> in Order, #genotype : #phenotype = 1 : 1
– One-dimensional vs multi-dimensional
One-dimensional encoding에서 각 chromosome은 일렬로 배열되며, 두 chromosome 사이의 연결성이 없습니다.
Multi-dimensional encoding에서 각 chromosome은 길이가 가변적인 여러 열로 배열됩니다. 이 유형의 인코딩은 대규모의 문제를 다루는 데 효과적입니다.
2. Operator
GA 연산자는 크게 4가지로 분류 할 수 있다
=> Selection, CrossOver, Mutation, Replacement(for steady-state GA)
2.1 Selection
Selection operator는 현재 세대(population) 에서 다음 세대을 생성하기 위한 parents(부모)를 선택하는 단계입니다.
이때, superior individuals(우수 개체)는 더 많은 선택 기회를 가지도록 만들어져야 하는데 inferior individuals(하위 개체)도 일정한 선택 기회를 가지도록 설정해야 합니다.
Roulette-wheel selection
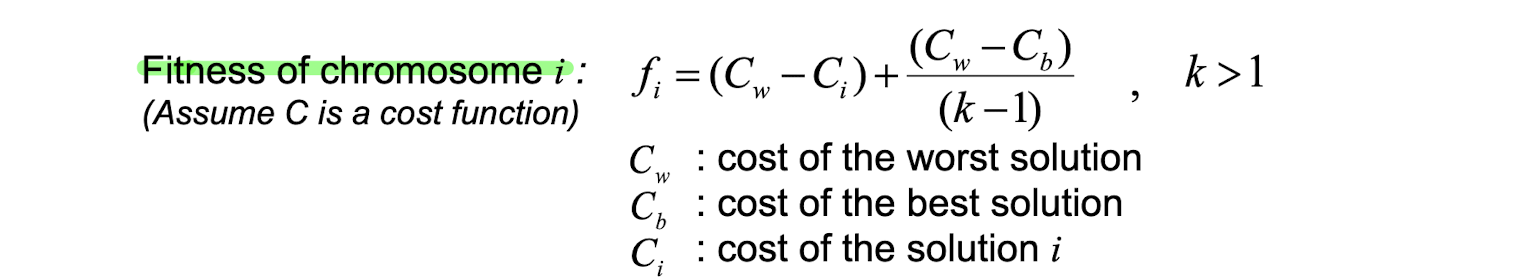
Roulette-wheel selection은 각 chromosome의 fitness value(적합도 값)을 기반으로 선택 기회를 할당하는 기본적인 방법입니다. 이 방법은 선택 기회와 fitness value 간의 비례 관계를 기반으로 하기 때문에, superior individuals에게 더 많은 선택 기회를 주어야 한다면 cost 함수를 이용하여 조정해야 합니다.
Adjusted roulette-wheel selection은 cost 함수를 이용하여 상대적인 선택 가능성(선택 확률)을 계산합니다. cost 함수는 fitness value를 가지고 각 chromosome이 상응하는 cost를 계산한 후, 선택 가능성이 높은 chromosome은 상대적으로 낮은 cost 값을 갖도록 조정됩니다.
이때, 최고 해(cost of the best solution), i번째 해(cost of the solution i), 최악 해(cost of the worst solution) 값을 이용하여 cost 값을 계산합니다. 또한, k 값에 따라 선택 가능성(선택 확률)을 격차를 크게 또는 작게 만들어주며, 일반적으로 3 또는 4를 사용합니다. ( K가 클수록 다양성은 떨어지고 , 적합성은 올라감 )
따라서, selection operator는 GA에서 중요한 부분 중 하나이며, adjusted roulette-wheel selection은 cost 함수를 이용하여 superior individuals가 더 많은 선택 기회를 갖도록 만드는 방법 중 하나입니다.
Rank-based selection
Rank-based Selection은 population 내에서 각 chromosome의 순위(rank)를 기반으로 fitness value(적합도 값을) 할당합니다. 이 방법은 어떤 상위집합 내에서 최고 집합을 신속하게 선택하고, 일부 좋은 quality의 해(loss function value가 작은 해)가 초기 세대에서 빨리 발견되는 것을 방지하여, 모델이 조기 수렴되는 것을 방지합니다.
Rank-based Selection에서는 각 chromosome의 fitness value를 다음과 같은 방식으로 할당합니다. fi는 i번째 chromosome의 fitness 값입니다. max와 min은 fitness 값의 최대 값과 최소 값입니다. n은 population의 총 개수입니다.
f_(i) = max + (i-1) * (min-max) / (n-1)
여기서, 제일 좋은 해(loss function value가 가장 낮은 해)의 fitness 값은 max 이며, 제일 나쁜 해(loss function value가 가장 큰 해)의 fitness 값은 min입니다. 따라서, 모든 fitness 값은 max와 min 값 사이에서 균일하게 분포됩니다.
selection power(선택력)는 max와 min 값을 조정하여 제어할 수 있습니다. max 값을 높이면 상위 집합(selected pool)은 더 큰 비율을 차지하게 됩니다. 반대로, min 값을 낮추면 상위 집합은 더 작은 비율을 차지하게 됩니다. 이 방법을 사용하면, 다양한 해를 생성하면서도 좋은 quality의 해를 선택할 수 있습니다.
2.2 CrossOver
1. Point cross-over
: 부모 염색체에서 랜덤한 지점을 선택하여 그 위치 이후의 염색체를 서로 교환하는 방식입니다.
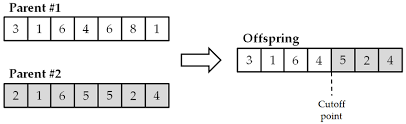
2. Multipoint cross-over
: 부모 염색체에서 랜덤한 지점 여러 개를 선택하여 그 위치 이후의 염색체를 서로 교환하는 방식입니다.
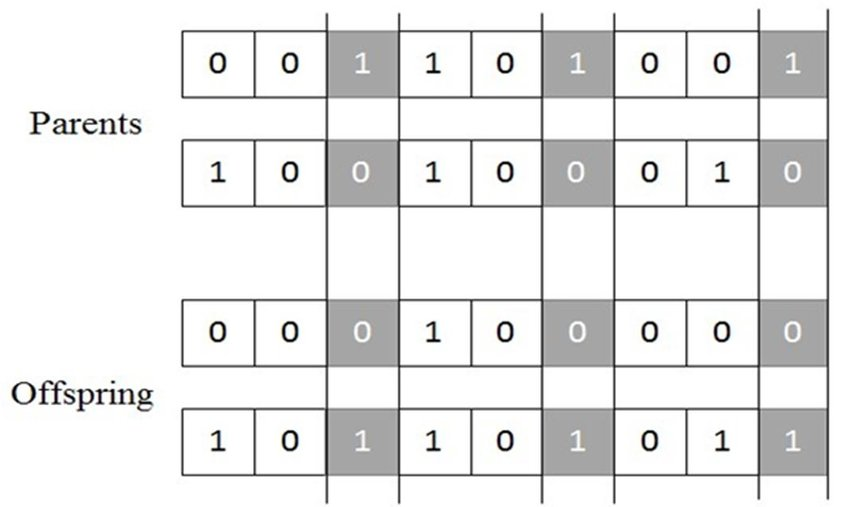
3. Uniform cross-over
: 부모 염색체에서 각각의 염색체에 대하여 일정한 확률로 서로 교환하는 방식입니다.

4. Cycle cross-over
두 부모 염색체를 순서대로 비교하면서 새로운 염색체를 생성하는 방식이다. 중복되지 않는 염색체를 선택하면서 교환하고, 처리되지 않은 염색체를 이용하여 새로운 염색체를 만들어나감. ( 순열로 나타낸 경우에 유용하고, 각 서브 사이클 마다 선택지 교환 )
5. Order cross-over
랜덤한 구간을 선택하여 그 구간 안에 있는 염색체를 상위에서 하위까지 명시한 순서대로 배치하는 방식입니다
6. PMX (Partially Matched cross-over)
두 개의 짝을 이루는 부모 염색체에서 랜덤하게 구간을 선택하고, 선택된 구간 내에서 유전자간의 대응관계를 유지하는 방식입니다.
7. Arithmetic cross-over
두 부모 염색체를 랜덤한 비율로 섞어서 새로운 염색체를 만들어내는 방식입니다. ( 실제 값 형태로 나타낼 때 유용함 )
8. Huristic cross-over
유전자 알고리즘에서 사용하는 다양한 전략을 조합하여 적용하는 방식입니다.
9. Multi-dimensional cross-over
다양한 유전자를 포함하는 염색체에 대해서 랜덤한 방향으로 구간을 선택, 구간을 서로 교환하여 새로운 염색체를 만들어내는 방식입니다.
10. Block-uniform cross-over
랜덤한 지점을 선택하여 그 위치 이후의 일정한 크기의 구간을 서로 교환하는 방식입니다. ( 그래프 형식의 데이터에서 유용 )
11. Geographic cross-over
연속한 구간을 선택하여 서로 교환이 이루어지는 방식으로, 유전자들 간의 순서가 중요한 문제에 대해 사용됩니다.
12. Natural cross-over
유전자 알고리즘에서 주로 사용되는 cross-over 전략으로, 가장 기본적인 방식으로, 부모 염색체를 랜덤한 지점에서 각각 교환하여 새로운 염색체를 만들어내는 방식입니다.
2.3 Mutation
변이는 부모 유전자의 특성을 보완하고 검색 공간을 적극적으로 이용하는 작업입니다.
- 전통적인 mutation 방식
전통적인 변이 방식은 각 유전자에 대해 임계값 이하의 랜덤한 수를 생성하고, 그 값이 임계값 이하이면 유전자를 변이시키고, 임계값 이상이면 유전자 값을 보존하는 식으로 이루어집니다.
또 다른 전통적인 변이 방식으로는 두 개의 유전자를 스왑하는 방식이 있습니다.
- non-uniform 적인 mutaion 방식
non-uniform 변이는 세대가 지나면서 변이 강도를 점점 줄이는 방식입니다.
non-uniform 변이 방식은 유전자들 간의 유사성을 유지시키는 것이 중요한 mimetic GAs에 적용하기에 적절하지 않을 수 있습니다.

2.5 Replacement
Replacement(대체)은 유전자 알고리즘(Genetic Algorithm)에서 새로운 해를 생성한 후, 이를 어떻게 기존의 해와 교체할지를 결정하는 작업입니다.
Steady-state GAs에서는 replacement 연산자가 효과적으로 평가받습니다.
전통적인 대체 방식은 열약한 해를 대체하는 것이다. 이 방식은 강한 수렴성을 가지지만, 일찍 수렴하는 위험이 있습니다.
- 엘리트 주의(elitism)는 최고 해를 유지하는 대체 방식으로, Steady-state GAs 와 세대 교체(GAG) 모두에 사용될 수 있습니다.
(또 다른 전통적인 대체 방식으로 두 개의 부모 중 더 나쁜 해를 대체하는 것이 있습니다. 자손이 둘 중 하나의 부모보다 우수하면, 그 부모를 대체하고, 그렇지 않으면 열약한 해를 대체합니다.)
- Crowding(인접성) 방식은 일부 인구를 선택한 후, 그 중 자손과 가장 유사한 해를 대체하는 것이다. 이 방식은 유전 진화의 다양성을 유지하는 데에 유용합니다.
* Control of diversity
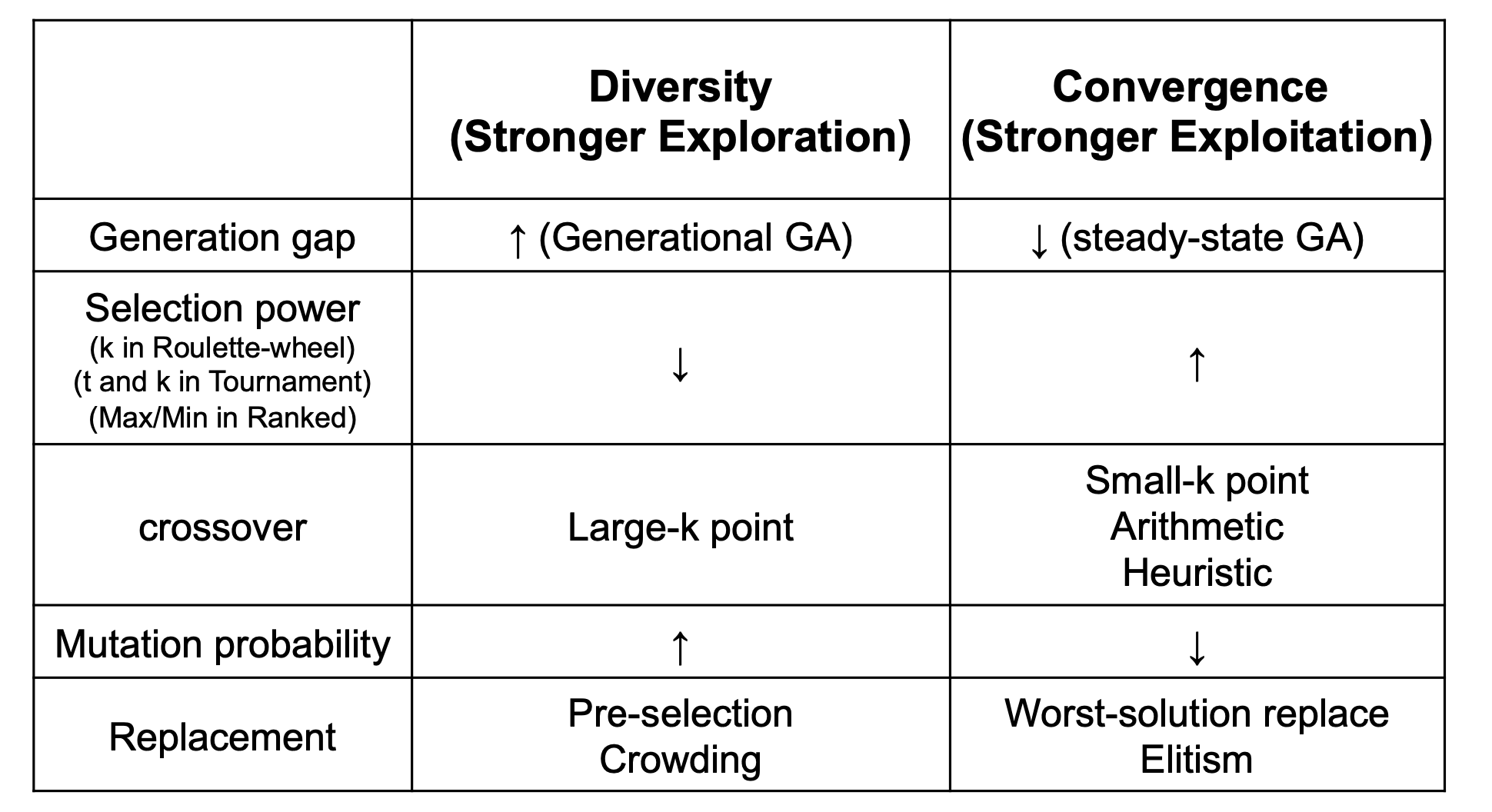
'Lab & Research > Artificial intelligence' 카테고리의 다른 글
| 머신러닝 알고리즘 - Naive Bayes (1) | 2023.12.29 |
|---|---|
| 머신러닝 알고리즘 - Logistic Regression (0) | 2023.12.18 |
| 머신러닝 알고리즘 - Linear Regression (0) | 2023.12.17 |
| Genetic Alogorithm 의 주요 이슈 (0) | 2023.06.19 |
| 진화 연산 개념 (0) | 2023.04.25 |



